13776 работ.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Без автора
Лекция одиннадцатая. О субъективности пространства
ЛЕКЦИЯ ОДИННАДЦАТАЯ.
О СУБЪЕКТИВНОСТИ ПРОСТРАНСТВА.
Восприятие пространства.—Теория Декарта и Беркли.—Роль осязательно-мускульного опыта в восприятии пространства.—Неогеометрия и доказательство мыслимости пространства в 4 и больше измерений.—Критика этого воззрения.—Субъективность пространства.
В прошлых двух лекциях мы рассмотрели вопрос о субъективности ощущений звука и цвета. Мы видели, что звук и цвет суть содержание наших ощущений. Разумеется, субъективность эту понимать нужно не в том смысле, что звук и цвет есть только ощущение, которому во внешнем мире ничего не соответствует, потому что в таком случае оно было бы иллюзией. Говоря, что ощущение звука и света субъективно, я хотел только сказать, что ощущению звука и света объективно соответствует нечто такое, что на них совершенно не похоже. Звук совсем не похож на разрежение и сгущение воздуха, цвет совсем не похож на волнообразные колебания эфира.
То же самое, что я говорил о звуке и цвете, приложимо и ко всем другим ощущениям. Сладости нет в сахаре, это есть наше ощущение; запаха, твердости, шероховатости, теплоты, холода и т. п. точно так же не существует в вещах; это суть наши ощущения.
Что ощущение не есть копия вещей, можно доказать при помощи следующих соображений. Солнечный луч, попадая в наш зрительный орган, доставляет нам ощущение света, тот же солнечный луч, ударяясь о поверхность нашей кожи, доставляет нам ощущение тепла. Капля уксуса, попадая на язык, доставляет нам ощущение кислого вкуса, на поверхности слизистой оболочки вызывает ощущение жжения. Один и тот же гальванический ток, проведенный через язык, вызывает кислый вкус, через глаз—ощущение красного или голубого цвета, через кожные нервы — ощущение щекотания, че-
171
рез слуховой нерв—ощущение звука 1). Следовательно, то обстоятельство, что мы имеем какое-либо ощущение, зависит не столько оттого, что производит возбуждение, сколько оттого, какой орган возбуждается, а отсюда мы можем сделать более общий вывод, что появление тех или других ощущений находится в зависимости, главным образом, от особенностей нашей организации. Если бы мы были устроены иначе, если бы наша физическая организация была иной, то, может быть, мир представился бы нам совсем в другом виде.
Кто-нибудь может возразить на это: «можно с вами согласиться в том, что такие свойства, как звук, цвет, запах, вкус и т. д., действительно, вещам не присущи, что они, действительно, существуют только лишь благодаря возбуждению тех или иных органов, но есть нечто такое, в объективности чего никто сомневаться не станет. Это именно пространство, протяженность, которое обладает несомненно существованием независимо от свойств нашей организации. Пространство есть нечто объективно существующее. Оно является, так сказать, носителем тех качеств, о субъективности которых только что была речь».
Хотя это замечание кажется и очень убедительным, но тем не менее с ним нельзя согласиться.
Чтобы решить вопрос, субъективно ли пространство, подобно указанным выше качествам вещей, нам нужно рассмотреть, каким образом мы воспринимаем пространство.
Орган, при помощи которого мы воспринимаем пространство, есть наш глаз, который по своему устройству напоминает камер-обскуру фотографа. От какого-либо предмета световые лучи проникают в наш глаз и в той части его, которая называется сетчаткой, отображаются, дают изображение, напоминающее собою самый предмет. Изображение это (разумеется, при прочих равных условиях) больше в том случае, если предмет больше; меньше в том случае, если предмет меньше; оно занимает одно место на сетчатке, когда предмет находится справа, другое в том случае, когда предмет находится слева; занимает одно место в том случае, если предмет находится снизу, иное в том случае, когда он находится сверху. Изображение одного и того же предмета больше, когда предмет находится близко от нас, оно меньше, когда предмет находится далеко от нас. Казалось бы, что таких изменений изображений на сетчатке вполне достаточно, чтобы мы могли руко-
1) Liemann. «Zur Analysis d. Wirklichkeit». 1880.
172
водствоваться ими при восприятии пространства, т.е. при восприятии величины, формы, положения и удаления предметов. Но в действительности это едва ли так.
Декарт, который был одним из первых занимавшихся исследованием этого вопроса, решал его следующим образом. Когда мы определяем расстояние предметов от нас, то мы пользуемся теми углами, которые зрительные линии образуют у нас в глазу. Если, напр., предмет находится близко и посылает лучи в оба наши глаза, то образуются два угла небольшие; если же предмет от нас удаляется, то углы эти становятся больше. Зная эти углы, мы и определяем расстояние предметов. Вот его слова: «Расстояние мы определяем, благодаря взаимному согласию обоих глаз (как бы по какой-то всем нам врожденной геометрии). Когда наши глаза RST и rst направляются к точке X, то величина линии Ss и углов XSs и XsS дают нам знать, где находится точка X (см. рис. 1)» 1).
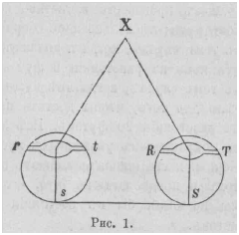
Против этой теории высказался английский философ Беркли в своей знаменитой книге «Новая теория зрения»
(1709). Он именно показал путем чрезвычайно остроумных рассуждений, что при помощи одного только зрительного аппарата мы совершенно не в состоянии определять расстояния предметов от нас, а равным образом и величины предметов.
Если какая-нибудь точка находится вне нас, то она в нашем глазу в известном месте отбрасывает изображение опять-таки в виде точки. Если эта точка удаляется, то на прежнем месте получается такое же изображение точки, как и прежде; если предмет удалится еще больше, то получится то же самое; следовательно, мы не можем определять расстояния точки при помощи изображений сетчатки, так как нет никакого различия между изображениями точки на сетчатке, приближается ли точка, или она удаляется. Если каждый предмет представляет собою не что иное, как совокупность точек, то мы легко поймем, что воспринять расстояние предметов при помощи изменения изображений на сетчатке мы не в состоянии.
1) Des Cartes. Dioptrices VI, 13.
173
Но фактически мы, ведь, при помощи глаза воспринимаем расстояние предметов. Как же примирить это кажущееся противоречие между рассуждением Беркли с одной стороны и фактическим восприятием расстояния с другой? Беркли думает, что мы можем воспринимать расстояния предметов только лишь потому, что мы, кроме зрительного опыта, имеем еще и так называемый осязательно-двигательный опыт.
Наш глаз снабжен шестью мускулами, из которых каждый своеобразно сокращается и растягивается при движении глаза в сторону, вверх, вниз, внутрь. Сокращение мускулов глаза вызывает так называемое мускульное ощущение. Это мускульное ощущение сопровождает сокращение и других мускулов нашего организма. Напр., если я желаю достать рукою предмет, находящийся от меня на расстоянии 1-го фута, то я должен произвести известное сокращение и растяжение мускулов руки; несколько иное сокращение и растяжение я произвожу в том случае, когда я должен достать предмет, находящийся от меня на расстоянии 3 футов, и совсем иные сокращения в том случае, когда мне нужно привести в движение все свое тело для того, чтобы достать предмет, находящийся от меня на расстоянии 20 футов. Все эти ощущения, которые связаны с сокращением указанных мускулов и передвижением тела, Беркли и его школа называют осязательно-мускульным опытом и предполагают, что, если бы не было этого опыта, то мы не были бы в состоянии воспринимать расстояния предметов.
Беркли думает, что главная доля в восприятии пространства принадлежит именно осязательному опыту; что мы научаемся определять величину и расстояние предметов первоначально при помощи осязательного опыта. К этому осязательному опыту присоединяется и зрительный опыт, т.е. зрительное ощущение. Осязательно-мускульное ощущение и зрительное ощущение, вследствие продолжительного опыта, связываются теснейшим образом друг с другом. Вследствие этого происходит то, что мы во взрослой жизни не пользуемся осязательным опытом, а пользуемся исключительно опытом зрительным. Зрительные ощущения делаются как бы знаками для того пространства, которое мы воспринимаем при помощи органов осязания.
Если это рассуждение Беркли и его школы 1) относительно
1) Более подробное изложение итого вопроса см. в моем сочинении: «Проблема восприятия пространства». Киев. 1896. Глава VII. «Зрение и осязание».
174
роли осязательных ощущений для восприятия пространства, может быть, не для всякого ясно, то доказательства роли осязательно-двигательных ощущений для восприятия пространства, которые приводятся в этом случае, очень убедительны.
Беркли между прочим в указанном выше сочинении задавался вопросом о том, какое существует отношение между пространством осязательным и между пространством зрительным, и думал, что между ними нет никакого сходства; что это два совершенно разнородных пространства; он думал, что, если бы слепой прозрел, то не был бы в состоянии воспринимать зрительного пространства.
Теоретические догадки Беркли подтвердились весьма скоро, именно в 1728 году доктором Чезельденом, который произвел удачную операцию над одним слепорожденным.
Надо знать, что иногда дети рождаются с катарактами или бельмами на обоих глазах. Это делает их слепыми. Но этн бельма при помощи хирургических приемов молено удалить, и бывшие до того слепыми прозревают. Первая операция такого рода, как я только что сказал, была совершена Чезельденом. Когда слепой Чезельдена впервые стал видеть, он очень дурно воспринимал расстояние: ему казалось, что предметы касались его глаз точно так, как они прикасаются к его коже. Он не мог узнать формы вещей до тех пор, пока не прикасался к ним.
После Чезельдена таких операций было произведено чрезвычайно много, но все они привели к одним и тем же результатам, они показали, что, хотя слепой тотчас после прозрения и может отличать контуры, но воспринимать расстояние предметов так, как это делает зрячий, он не в состоянии.
Довольно любопытным является больной, которому совершил операцию проф. Рельман в Дерпте 28 апреля 1890 года. Спустя несколько времени после прозрения, пациенту показывают фарфоровую чашку и фарфоровый же сосуд одинаковой формы, но в десять раз больше, чем чашка; первый держат на расстоянии 11/2 метра, второй на расстоянии 8 метров; оба предмета признаются тождественными; посредством осязания он узнает чашку.
1 мая пациенту показывают шар и куб, оба из одинаково окрашенного дерева, имеющие один и тот же диаметр. Когда их ставят рядом, то он видит, что они различны, во не может сказать, который предмет круглый и который из чих имеет углы. Рядом с шаром ему показывают кружок,
175
а рядом с кубом четыре уголь ник (разумеется, соответственных размеров). Пациент не мог отличить куба от четырехугольника, шара от круга; различает только после ощупывания. При выздоровлении он совершенно своеобразно упражнялся в смотрении: он, напр., снимает сапог с ноги, бросает на известное расстояние от себя и затем старается определить расстояние, на котором находится сапог, делает несколько шагов по направлению к сапогу и старается схватить его, и если это не удается, то делает еще несколько шагов, пока, наконец, не схватит. Он очень занят больным, который находится с ним в одной комнате, старается изучить его, ощупывает его голову, руки, отдельные части лица, в то время как наблюдает их посредством глаз 1).
Из приведенных примеров ясно, что прозревший слепорожденный не может воспринимать пространства посредством одного только зрения. Отсюда следует, что восприятие пространства необходимо совершается как при содействии зрительного, так и осязательного опыта.
То же самое положение доказывается и наблюдениями над новорожденными. Новорожденные в первые дни жизни не только не могут воспринимать расстояния предметов, но даже единственно, что они могут различать—это известные оттенки светлого и темного. Как медленно совершенствуется у них зрение или способность восприятия пространства, показывает то обстоятельство, что ребенок на 18-й неделе жизни протягивает руку к предметам, находящимся от него на двойном расстоянии руки, что ясно указывает на то, как дурно оценивается им расстояние, вследствие того, что он до сих пор слишком мало пользовался осязательным опытом.
Этих соображений, я думаю, достаточно, чтобы видеть, что представление пространства складывается из нескольких ощущений: из зрительного, осязательного и мускульного.
Теперь мы легко можем ответить на поставленный нами выше вопрос. Если те ощущения, которые входят в составь представления пространства, носят характер субъективный, то, само собою, разумеется, что и представление пространства должно обладать характером субъективным, подобно тому, как таковым отличалось ощущение звука, цвета и т. п.
Таким образом, мы видим, что между представлением пространства и ощущениями звука, цвета и др. можно провести полную аналогию.
1) «Zeitschrift für Psychologie». В. II.
176
Но не можем ли мы провести аналогию дальше и спросить, не находимся ли мы, в случае восприятия пространства, в таком же положении, в каком мы находимся, когда ощущаем, напр., цвет, звук? Не можем ли мы сказать, что восприятие пространства так же обусловливается нашей психофизической организацией, как ощущение цвета и звука обусловливается нашей физической организацией? Не можем ли мы пойти дальше и спросить, существует ли пространство независимо от нашего восприятия? Существует ли оно, как говорят философы, абсолютно, или же оно всецело обусловливается нашей психофизической организацией, т.е. если бы наша организация была иная, то и пространство было бы иным? Решение этого вопроса представляет огромные трудности. Но чтобы не пройти его совсем молчанием, я познакомлю вас с учением о мыслимости пространств иных форм в сравнении с нашим. Разобравши рассуждения сторонников этого учения, мы отрицательным путем придем к выводу, что представление нашего пространства самым неразрывным образом связано с нашей психофизической организацией, или что, другими словами, форма нашего представления пространства обусловливается нашей психофизической организацией в том же смысле, в каком ощущение цвета обусловливается нашей физической организацией.
Учение о мыслимости иных пространственных отношений, в сравнении с нашим, содержится в так наз. метагеометрии, сущность которой сводится к следующему.
Как известно, геометрия состоит из таких положений, которые неоспоримы, обладают абсолютной достоверностью. Никто не стал бы оспаривать, напр., таких положений геометрии, как то, что площадь треугольника равняется половине произведения основания на высоту, что площадь круга равняется πr2. На чем же основана достоверность положений геометрии? На том, что она дедуктивным путем выводит свои положения из так называемых аксиом и определений, которые отличаются абсолютной достоверностью. Кто стал бы сомневаться или требовать доказательства такой аксиомы, что «две величины, порознь (равные третьей, равны между собой», или оспаривать определение, что «прямая линия есть кратчайшее расстояние между двумя точками». На достоверности этих аксиом и определений основывается достоверность всех остальных выводных положений геометрии. Этим объясняется также и то, что наша современная геометрия есть геометрия, написанная греческим математиком Евклидом за 2.000 лет до нашего времени.
Но между теми аксиомами, которые нам завещала греческая
177
геометрия, есть одна, так называемая одиннадцатая аксиома Евклида, которая всегда вызывала сомнения у математиков. Как известно, эта аксиома выражается следующим образом: «перпендикуляр и наклонная при продолжении встретятся», или «если нам дана линия и вне ее точка, то через эту последнюю можно провести только одну линию, ее не встречающую (параллельную)». Геометры думали, что это собственно не аксиома, а теорема, и прилагали все усилия к тому, чтобы найти для нее доказательства; но усилия их были тщетны: такого доказательства найти нельзя было.
Но вот в тридцатых годах текущего столетия русский математик Лобачевский решил, что, если эта аксиома доказана быть не может, то нужно предположить, что она не действительна, другими словами, нужно предположить, что, если нам дана линия и вне ее точка, то через эту точку можно провести бесконечное множество прямых, не встречающих первую. Сделав такое предположение, т.е. допустив, что 11-я аксиома Евклида недействительна, он сделал все те выводы, какие только можно было сделать из этого предположения, и получилась новая геометрия с многочисленными теоремами и доказательствами, получилась особая геометрия, построенная при предположении, что одиннадцатая аксиома Евклида недействительна.
Из этого построения вывод был очевиден: наша геометрия есть частный вид другой, так сказать, абсолютной геометрии. Абсолютная геометрия—это та, которая строится при предположении недействительности 11-й аксиомы, а наша евклидовская строится при ограничительном условии, что 11-я аксиома действительна 1).
Эта идея Лобачевского оставалась долгое время непризнанной, и только после того, как немецкие ученые Риман и Гельмгольц воскресили эту идею, придав ей философский характер, она обратила на себя всеобщее внимание 2).
Философский характер принадлежал этой идее потому, что, казалось, если существует геометрия, отличающаяся от нашей евклидовской, то остается вполне мыслимым существование других пространств с совершенно иными свойствами, не-
1) Лобачевский (Собр. соч., стр. 79) абсолютную геометрию называет «воображаемой». По его мнению, «воображаемая геометрия обнимает употребительную геометрию, как частный случай». См. также Frischauf. «Elemente d. absoluten Geometrie». 1873, стр. 106 и д.
2)См. Helmholtz. «Vorträge und Reden». (Популярные речи. Спб. 1898). Его речь «Об аксиомах геометрии» представляет популярное изложение вопроса.
178
жели наше. Усилия философов-математиков были направлены на то, чтобы показать, что мыслимы пространства иной формы, чем наше. Заметьте логический ход мысли. Если возможна другая геометрия, то, значит, возможны и другие пространства, или пространственные отношения, потому что геометрия является выражением этих последних.
Эту мыслимость, по их мнению, можно доказать следующими соображениями; именно, можно показать, что наши аксиомы, составляющие фундамент нашей геометрии, отличаются далеко не всеобщей приложимостью. Возьмем следующие три аксиомы: во-первых, аксиому совместимости, по которой величины, совпадающие друг с другом, равны; во-вторых, аксиому, по которой «две точки определяют положение прямой», или по которой «между двумя точками можно провести только одну прямую», и, наконец, возьмем также аксиому параллельности и рассмотрим, на каких поверхностях все эти аксиомы имеют приложимость. Тогда окажется, что есть поверхности, на которых одни аксиомы имеют приложимость, а другие нет.
Возьмем, прежде всего, аксиому совместимости 1). Кажется само собою очевидным, что мы в любом пространстве можем убедиться в равенстве геометрических фигур между собою, если только они совпадают друг с другом. Но в действительности, чтобы мы могли производить совпадение или совмещение, мы должны быть убеждены в том, что тело или фигура при своем перемещении не изменяются в зависимости от самого пространства, другими словами, мы должны быть убеждены, что величина фигуры не зависит от ее положения в той или другой части пространства, в том или другом роде пространства. Это непонятное на первый взгляд положение сделается для вас тотчас ясным, если мы рассмотрим приложимость аксиомы совместимости на разных поверхностях. Конечно, на плоскости эта аксиома имеет полную приложимость: где бы, на каком бы месте ее мы не имели треугольник, мы можем его переместить на другое место, при чем он не изменит своей величины. Если мы возьмем поверхность цилиндра или конуса, то на ней аксиома совместимости тоже имеет место. Треугольник, начерченный в одной части поверхности цилиндра и конуса, можно передвигать по всей их поверхности, при чем фигура, передвигаясь без складок и растяжении,
1) Некоторые называют эту аксиому «аксиомой свободной подвижности». Напр., Kussel. «The Foundations of Geometry». 1S97. Это название мне кажется более выразительным.
179
будет сохранять одну и ту же величину. На поверхности шара аксиома, совместимости также имеет приложимость. На пей треугольник или какая-нибудь другая фигура может, опять-таки без складок и растяжений, передвигаться и, стало быть, совпадать с равной ей фигурой. Но есть поверхности, на которых аксиома совместимости не имеет места, такова, напр., поверхность яйцеобразная. Если на тупом конце этой последней поверхности мы начертим треугольник, то мы не можем его передвинуть к острому концу без того, чтобы не образовалось в фигуре складок. То же нужно сказать и о поверхности эллипсоида. Таким образом, мы видим, что на поверхности эллипсоида фигура не может передвигаться, не изменяя своей фигуры. Если так, то на поверхности эллипсоида нет совмещения тел. Там нет равенства фигур. А отсюда ясно, что первая наша аксиома имеет не повсеместное приложение.
Возьмем вторую аксиому. На плоскости между двумя точками можно провести только одну прямую, т.е. кратчайшее расстояние между двумя точками. То же самое можно сказать и относительно поверхности конуса и цилиндра. На поверхности шара кратчайшая линия, как известно, есть дуга большого круга; но нельзя сказать относительно поверхности шара, что на ней между двумя точками всегда можно провести только одну кратчайшую. В действительности на поверхности шара есть точка, между которыми можно провести бесчисленное множество кратчайших расстояний. Представьте себе две точки полюсов. Через них можно провести бесчисленное множество меридианов или кратчайших расстояний между полюсами. Следовательно, и эта аксиома имеет не повсеместную приложимость.
Возьмем далее аксиому параллельности. На плоскости из точки, находящейся вне прямой, можно провести только одну прямую, не встречающую первой. То же самое на поверхности цилиндра и конуса. Но эта аксиома не имеет места на поверхности шара. На поверхности шара вне одной кратчайшей нельзя провести другой кратчайшей, которая не встречала бы этой последней. Напр., два меридиана представляют собою две кратчайших прямых, перпендикулярных к третьей, но, как известно, они всегда встречаются у полюса.
Есть еще одна замечательная поверхность, которая во всех отношениях похожа на нашу плоскость, только аксиома параллельности на ней не имеет места. На рис. 2-м изображается один из видов этой поверхности. Это поверхность бокала с удлиненным концом.
Эту поверхность называют псевдосферой. На псевдосфере
180
аксиома совместимости имеет приложимость. На ней фигуры могут передвигаться без изменения своей величины: на ней между двумя точками можно провести только одну кратчайшую, но зато на ней, если дана кратчайшая и вне ее точка, то через эту точку можно провести бесчисленное
множество кратчайших линий, не встречающих первую. Т.е., другими словами, на псевдосфере аксиома параллельности не имеет места; а так как с аксиомой параллельности тесно связано то положение, что сумма углов в треугольнике равняется 2d, то сумма углов треугольника на псевдосфере не равняется 2d, а меньше. На псевдосфере нет подобия треугольников, потому что на ней чем больше стороны треугольника, тем меньше сумма углов, и наоборот.
 Таким образом, рассмотрев приложимость различных аксиом к различным поверхностям, мы находим, что геометрические аксиомы имеют различный характер, смотря по поверхности; на одних поверхностях действительны одни аксиомы, на других—другие, в зависимости от того, какими свойствами обладает сама поверхность. Геометрия изменяется в зависимости от поверхностей.
Таким образом, рассмотрев приложимость различных аксиом к различным поверхностям, мы находим, что геометрические аксиомы имеют различный характер, смотря по поверхности; на одних поверхностях действительны одни аксиомы, на других—другие, в зависимости от того, какими свойствами обладает сама поверхность. Геометрия изменяется в зависимости от поверхностей.
Но если наше рассуждение относительно возможности иной геометрии, нежели наша, справедливо применительно к поверхностям, т.е. пространствам двух измерений, то оно может быть применимо по аналогии и к пространству большего числа измерений 1). Мы можем мыслить существование таких пространств, больше чем в два измерения, в которых действуют совсем не те законы, какие действуют в нашем пространстве.
Может быть, с другой стороны, наше пространство в
1) Более полное изложение этого вопроса, чем можно было дать в этой книге, читатель может найти в соч. Benno-Erdmann'a. «Die Axiome der Geometrie». 1877. Новейшее состояние вопроса в книге Russel’я «The Foundations of Geometry». 1897, а также в моей книге: «Проблема восприятия пространства», ч. 2-я.
181
действительности обладает не теми свойствами, какие мы ему приписываем.
Чтобы пояснить основательность такого допущения, предположим следующее. Предположим поверхность шара с настолько большим радиусом, что она почти приближается к плоскости. Предположим, что на этой поверхности живут существа, занимающиеся геометрией. Допустим, что два существа, живущие на этой поверхности и не знающие, на какой поверхности они находятся, выходят из двух точек экватора и движутся перпендикулярно экватору по кратчайшей линии. Если бы они задались вопросом, встретятся ли когда-нибудь, то они, конечно, ответили бы на этот вопрос отрицательно; но, как мы знаем, они ошиблись бы: они должны встретиться у полюсов. Но отчего же у них произошла такая ошибка? Оттого, что, исследовав часть своего пространства, они решились рассуждать о своем пространстве в целом.
Не находимся ли мы точно так же в положении этих геометров? исследовав часть нашего пространства, мы в действительности не можем рассуждать о нем в целом. Может быть, если бы мы исследовали его во всем его объеме, то оказалось бы, что оно обладает вовсе не теми свойствами, какие мы ему приписываем. Мы, например, думаем, что две параллельные линии никогда не встретятся, но полного логического основания для такого утверждения у нас нет. Может быть, если бы мы эти линии стали бесконечно продолжать, то они где-нибудь встретились бы. Свойства нашего пространства следует определить эмпирически. Так думали Риман и Гельмгольц.
Какое же средство они предлагали для определения истинных свойств нашего пространства? Они думали, что, если бы построить треугольник с очень большими сторонами и измерить сумму его углов, тогда можно было бы решить интересующую пас задачу. Если бы, например, оказалось, что сумма углов в таком треугольнике не равняется двум прямым, то мы могли бы сказать, что наше пространство в действительности не есть евклидовское. Такой треугольник мы можем получить в астрономических наблюдениях. Когда определяется расстояние какой-либо звезды от земли, то сначала определяется угол, под которым она видна в один момент, а затем в другой момент полгода спустя. Тогда у пас получается треугольник, основанием которого является ось земной орбиты. В таком треугольнике можно определить сумму углов. Правда, исследования Лобачевского относительно суммы углов в таком
182
треугольнике 1), не дали таких результатов, на основании которых можно было бы думать, что наше пространство имеет не те свойства, какие мы ему приписываем, но, тем не менее, Гельмгольц предполагает, что, если бы мы имели треугольник больший, чем тот, о котором только что была речь, то, может быть, результаты получились бы иные 2).
Исходя из того положения, что наше пространство, может быть, есть только частный вид пространства вообще, Гельмгольц и Риман старались обобщить самое понятие пространства; они старались показать, что есть более общее понятие, которое обнимает понятие пространства. Это именно понятие многообразия.
Вводя это понятие, они хотели сказать, что мыслимо не только пространство в три измерения, но и в четыре и т. д. измерений. Это легко пояснить следующим образом.
Отчего мы линии приписываем одно измерение? Оттого, что на ней мы можем определить положение какой-либо точки при помощи одного данного (при помощи длины линии от этой точки до другой).
Отчего мы плоскость называем пространством в два измерения? Как известно, оттого, что положение точки на плоскости определяется при помощи двух перпендикуляров, опущенных на стороны прямого угла. Эти перпендикуляры, как известно, называются координатами. Отчего мы наше пространство считаем пространством в три измерения? Оттого, что положение точки в нашем пространстве мы определяем при помощи трех координат. Если мы определяемость при помощи того или другого количества данных положим в основу понятия многообразия, то мы поймем, что, например, музыкальный тон есть многообразие двух измерений, потому что для нас достаточно двух данных для того, чтобы определить положение одного музыкального тона среди всех других. Если нам скажут, что музыкальный тон имеет такую-то высоту и такой то тембр, то мы тотчас можем определить этот тон. В этом смысле можно сказать, что система цветов представляет собою многообразие трех измерений потому, что трех данных
1) Из его исследований оказалось, что сумма углов в таком треугольнике на 0,0003 сек. меньше двух прямых (Лобачевский, Собр. соч., стр. 79). Эта неточность может находиться в зависимости от несовершенства измерительных приборов.
2) Гаусс хотел воспользоваться построением другого рода треугольников для той же цели. Об этом см. Klein. «Nicht-Euclidische Geometrie». 1893, ч. 1-я, стр. 163-4.
183
(цветовой тон, яркость и насыщенность) вполне достаточно, чтобы определить положение того или другого цвета среди всех остальных цветов.
Отсюда легко понять, что пространством в четыре или пять измерений мы должны назвать такое пространство, в котором положение той или иной точки определяется при помощи четырех, пяти и т. д. координат 1).
Из всех этих рассуждений, по-видимому, следует, что мыслимы пространства других видов, чем то, которое мы воспринимаем. Некоторые шли дальше и утверждали, что пространства больше, чем в три измерения, не только мыслимы, но и возможны 2).
Но будет ли правильно, если мы сделаем вывод, что представимо пространство иных форм, чем наше? Я думаю, что нет. Из вышеприведенных рассуждений мы можем сделать только тот вывод, что пространство в четыре измерения может быть изобразило при помощи формул; при помощи формул мы можем изобразить пространство во сколько угодно измерений, но мыслить или представить пространство в четыре измерения так, как мы представляем наше пространство в три измерения, мы не можем.
Я на одном примере покажу вам, как мы можем изобразить пространственные отношения чуждого нам вида пространства при помощи формул. Напр., для изображения расстояния на плоскости, по Пифагоровой теореме, мы будем иметь следующую формулу: δ = ![]() x12+x12. Для изображения расстояния диагонали параллелепипеда, т.е. в пространстве в три измерения, мы имеем формулу δ = и
x12+x12. Для изображения расстояния диагонали параллелепипеда, т.е. в пространстве в три измерения, мы имеем формулу δ = и![]() x12+x12+x32. Отсюда для пространства в четыре измерения мы, изменяя
x12+x12+x32. Отсюда для пространства в четыре измерения мы, изменяя
1) Один философ утверждал, что в пространстве в четыре измерения в каждой точке могут быть построены четыре перпендикулярных друг к другу линии.
2) Гельмгольц, по словам Либмана (Zur Analysis d. Wirklichkeit, 1880, стр. 62—3), в частной беседе с ним высказался в том смысле, что «возможно, что вне нашего сознания существует мир больше, чем из трех измерений». (Ср. с этим, впрочем, Helmholtz, Wissenschaftliche Abhandlungen. В. II, стр. 640, в прим.). Типичным в этом отношении является взгляд физика Тэта, который предполагает, что пространство нашей вселенной не везде имеет одни и те же свойства. «Возможно,— говорит он,—что при быстром движении солнечной системы в пространстве, мы постепенно перейдем, может быть, к областям, где пространство не имеет тех свойств, что здесь... где оно обладает свойствами, которые могут заставить вещество принять местами четвертое измерение...» (О новейших успехах физических знаний 1877. стр. 5).
184
предыдущие формулы по аналогии, будем иметь формулу δ =![]() x12+x12+x32+x42. Точно также мы получим формулу для пространства п измерений. Таким образом ясно, что изобразить мы можем пространства больше, чем в три измерения. Даже больше, мы можем задать себе вопрос относительно того, может ли в этих пространствах совершаться движение, если да, то по каким законам? Математики на этот вопрос отвечают, что движение возможно: они даже нашли формулы, но которым совершается это движение, и именно, видоизменяя по аналогии формулы движений в нашем пространстве. Очевидно, следовательно, что мы можем различные пространственные формы изобразить при помощи формул; но следует ли отсюда, что мы эти пространственные формы можем представить? Конечно, нет.
x12+x12+x32+x42. Точно также мы получим формулу для пространства п измерений. Таким образом ясно, что изобразить мы можем пространства больше, чем в три измерения. Даже больше, мы можем задать себе вопрос относительно того, может ли в этих пространствах совершаться движение, если да, то по каким законам? Математики на этот вопрос отвечают, что движение возможно: они даже нашли формулы, но которым совершается это движение, и именно, видоизменяя по аналогии формулы движений в нашем пространстве. Очевидно, следовательно, что мы можем различные пространственные формы изобразить при помощи формул; но следует ли отсюда, что мы эти пространственные формы можем представить? Конечно, нет.
Но отчего же не представимы для нас пространства других форм?
Оттого, что наша психофизическая организация такова, что мы пространство, отличное от нашего, воспринимать не в состоянии. Восприятие пространства обусловливается нашей организацией так же, как и восприятие звуков и цветов. То обстоятельство, что мы не можем себе представить другого пространства, является доказательством того, что наше представление пространства самым тесным образом связано с нашей психофизической организацией. Иное пространство для нас не представимо по той же причине, по которой для нас не представимо восприятие других цветов и звуков, кроме тех, которые мы воспринимаем. Если представление нашего пространства обусловлено нашей организацией, то оно субъективно в том же смысле, в каком субъективным является ощущение цвета и звука.
Следовательно, мы не должны думать, что пространство наше имеет абсолютное, независимое от нашего субъекта существование; напротив, оно всецело им обусловливается. В этом смысле наше пространство существует только для нас, только для нашего субъекта; для другого сознания нашего пространства, может быть, вовсе не существовало бы.
Пространство, следовательно, так же субъективно, как звуки и цвета.
185
© Гребневский храм Одинцовского благочиния Московской епархии Русской Православной Церкви. Копирование материалов сайта возможно только с нашего разрешения.
